Two-step equations are foundational algebraic problems requiring two operations to solve. They build on basic math skills, enhancing problem-solving abilities and logical thinking. Worksheets simplify practice and mastery.
1.1 What Are 2-Step Equations?
Two-step equations are algebraic expressions requiring two operations to isolate the variable. They involve combining or separating quantities through addition, subtraction, multiplication, or division. For example, solving (3x + 4 = 10) requires subtracting 4 and then dividing by 3. These equations build on basic algebra skills, introducing multi-step problem-solving. Unlike one-step equations, they demand a deeper understanding of inverse operations and sequential reasoning. Mastering 2-step equations is crucial for advancing in algebra and higher-level math. Worksheets and practice problems are essential tools for developing proficiency in identifying and applying the correct sequence of operations to find the solution.
1.2 Importance of Mastering 2-Step Equations
Mastering 2-step equations is essential for building a strong foundation in algebra and problem-solving. These equations introduce students to multi-operation scenarios, enhancing their critical thinking and mathematical fluency. Proficiency in 2-step equations prepares learners for more complex algebraic concepts, such as solving quadratic equations and systems of equations. In real-world applications, understanding these equations helps in budgeting, cooking, and science. They also improve logical reasoning and sequential thinking, which are valuable skills in everyday problem-solving. Worksheets and practice problems are vital tools for reinforcing these skills, ensuring students can apply inverse operations confidently and accurately. This mastery fosters a smooth transition to higher-level mathematics and STEM fields.
1.3 Transition from 1-Step to 2-Step Equations

Moving from 1-step to 2-step equations involves understanding the sequence of operations. In 1-step equations, a single operation is reversed, such as division to solve 2x = 6. For 2-step equations, like 3x + 5 = 20, you must first subtract 5, then divide by 3. This transition requires applying inverse operations in reverse order, following the mathematical order of operations. Worksheets are invaluable for practicing this process, helping to build confidence and fluency. By mastering this transition, learners can tackle more complex algebraic problems with ease, laying a strong foundation for future mathematical concepts.

Basic Steps to Solve 2-Step Equations
Solving 2-step equations involves reversing operations in the correct order. First, identify the operations applied to the variable. Then, apply the inverse operations in reverse order to isolate the variable. Always check your solution by substituting it back into the original equation to ensure both sides are equal. This methodical approach ensures accuracy and helps avoid common errors, such as misapplying signs or reversing operations incorrectly. Regular practice with worksheets can enhance proficiency and confidence in solving these equations effectively.
2.1 Identifying the Operations Involved

Identifying the operations in a 2-step equation is the first step toward solving it. Look for addition, subtraction, multiplication, or division applied to the variable. For example, in the equation 3x + 5 = 11, multiplication and addition are involved. Recognizing these operations helps determine the order of steps needed to isolate the variable. Worksheets often include equations with clear operation indicators, making it easier to practice this skill. Accurately identifying operations ensures the correct reversal process, avoiding errors like misapplying signs or reversing operations out of order. This foundational step is crucial for building confidence and proficiency in solving 2-step equations effectively.
2.2 Reversing the Order of Operations
Reversing the order of operations is essential for isolating the variable in 2-step equations. Start by undoing the last operation applied to the variable. For example, in the equation 3x + 5 = 11, subtraction is used to reverse the addition. This step simplifies the equation to 3x = 6. Next, division reverses the multiplication, yielding x = 2. Worksheets often provide structured examples to practice this reversal process. It’s crucial to perform operations in the correct order to avoid errors. Common mistakes include reversing operations out of sequence or misapplying signs, which can lead to incorrect solutions. Mastering this step builds a strong foundation for solving more complex equations with confidence and accuracy.

2.3 Checking the Solution
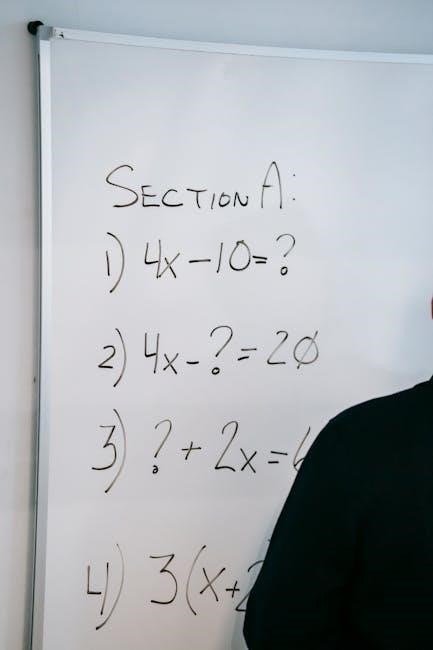
Checking the solution is a critical step in solving 2-step equations. After finding the value of the variable, substitute it back into the original equation to verify equality. For example, if solving 2x + 4 = 12 yields x = 4, plug x = 4 back in to confirm that 2(4) + 4 = 12, which simplifies to 12 = 12. This step ensures the solution is correct and helps identify any calculation errors. Worksheets often include space for this verification process, reinforcing the importance of accuracy. Regularly checking solutions builds confidence and reduces mistakes, making it a vital habit for mastering algebraic problem-solving skills. This practice also deepens understanding of equation balance and variable representation.

Common Types of 2-Step Equations
Two-step equations often involve combinations of addition, subtraction, multiplication, and division. They may include mixed operations, requiring students to apply inverse operations in the correct order to solve for the variable.
3.1 Equations Involving Addition and Multiplication
Equations involving addition and multiplication are common in 2-step problems. These equations typically require students to first undo an addition or multiplication operation before solving for the variable. For example, in an equation like 3x + 5 = 11, the student must first subtract 5 from both sides to isolate the term with the variable. After that, they divide by 3 to find the value of x. Worksheets often include a variety of these problems to help students practice reversing operations in the correct order. Mastering these types of equations builds a strong foundation for more complex algebraic concepts. Regular practice with such problems ensures proficiency and confidence in solving them accurately.
3.2 Equations Involving Subtraction and Division
Equations involving subtraction and division require a systematic approach to isolate the variable. For instance, in an equation like 12 = y / 3 – 4, the first step is to eliminate the subtraction by adding 4 to both sides. This simplifies the equation to 16 = y / 3. Next, to reverse the division, multiply both sides by 3 to solve for y, resulting in y = 48. Worksheets often include such problems to help students practice reversing these operations in sequence. These exercises enhance understanding of inverse operations and the importance of order in solving equations. Regular practice with these types of problems builds fluency and accuracy in algebraic manipulation.
3.3 Mixed Operation Equations
Mixed operation equations combine addition, subtraction, multiplication, and division, requiring careful step-by-step solving. For example, in 15 = 3x + 6, first subtract 6 from both sides to isolate the term with the variable, resulting in 9 = 3x. Then, divide both sides by 3 to solve for x, yielding x = 3. Worksheets often include such problems to help students practice handling multiple operations in sequence. These exercises reinforce the importance of the order of operations and the need to reverse them correctly when solving equations. Regular practice with mixed operation equations builds confidence and proficiency in algebraic problem-solving, preparing students for more complex mathematical concepts.
Solving 2-Step Equations Worksheet PDF
Downloadable PDF worksheets offer structured practice for mastering 2-step equations. They provide varied problems, solutions, and tips, aiding students and teachers in effective learning and instruction.
4.1 Locating Reliable Worksheets Online
Finding reliable worksheets for solving 2-step equations is essential for effective practice. Start by searching educational websites like MathWorks or Khan Academy. Use specific keywords such as “2-step equations worksheet PDF” or “solving 2-step equations practice problems” to narrow your search. Check the credibility of the source by reviewing the publisher and user reviews. Many worksheets are designed by teachers or educational institutions, ensuring quality content. Additionally, platforms like Teachers Pay Teachers offer curated resources. Always preview the worksheet to ensure it aligns with your skill level and covers the necessary topics. Downloading from trusted sites guarantees accurate and relevant practice materials.
4.2 Creating Custom Worksheets
Creating custom worksheets for solving 2-step equations allows for personalized learning. Use tools like Google Sheets or Microsoft Excel to design structured layouts. Start by defining the problem set, ensuring equations vary in difficulty and operations. Incorporate a mix of addition, subtraction, multiplication, and division to cover all scenarios. Add answer keys for self-assessment. Customize fonts, colors, and spacing for readability. Save the document as a PDF for easy sharing and printing. This method ensures relevance to individual learning needs, making practice more effective. Teachers and students can benefit from tailored resources that align with specific curriculum goals or skill levels. Regular updates keep the content fresh and challenging.
4.3 Benefits of Using Worksheets
Worksheets are an essential tool for mastering 2-step equations, offering structured practice and clear problem sets. They provide a focused environment for students to apply their skills, reducing distractions and enhancing concentration. Worksheets cater to different learning paces, allowing individuals to work independently. They also serve as valuable resources for homework or revision, ensuring consistent practice. Answer keys enable self-assessment, helping students identify and correct mistakes. Regular use of worksheets builds confidence and fluency in solving equations. Additionally, they are easily shareable and printable, making them a convenient option for both teachers and learners. Worksheets are a cornerstone of effective math education, fostering a deeper understanding of algebraic concepts.
Teaching Strategies for 2-Step Equations
Effective strategies include breaking down problems, using visual aids, and incorporating real-world examples. Interactive activities and scaffolding techniques enhance understanding and engagement for diverse learners.
5.1 Scaffolding Techniques
Scaffolding involves breaking down complex tasks into manageable steps, allowing students to build skills progressively. For 2-step equations, start with simple problems, then introduce more complexity. Use visual aids like diagrams or step-by-step guides to make abstract concepts concrete. Provide examples and guide students through initial problems, gradually reducing support as confidence grows. Incorporate worksheets with structured exercises that isolate each step, helping students master one operation before combining them. Tailor scaffolding to class needs, ensuring each student receives appropriate support. This approach fosters independence and deep understanding, making it easier for students to apply their knowledge to various problems, including those found in worksheets.
5.2 Using Visual Aids
Visual aids are powerful tools for teaching 2-step equations, helping students visualize abstract concepts. Diagrams, flowcharts, and algebra tiles can break down problems into clear, manageable steps. These tools allow students to see how operations interact and how reversing them leads to solutions. Color-coded representations can highlight different operations, making it easier for learners to identify and sequence steps. Interactive whiteboards and digital tools also enable real-time demonstrations, engaging students and clarifying complex ideas. Worksheets with visual supports, such as number lines or balance scales, further reinforce learning. By connecting equations to tangible visuals, teachers can help students develop a deeper understanding and improve their problem-solving skills.
5.3 Incorporating Technology
Incorporating technology into teaching 2-step equations enhances engagement and understanding. Interactive math software and online platforms provide step-by-step solutions, allowing students to explore problems at their own pace. Simulations and virtual manipulatives, like algebra tiles, offer visual representations of equations, making abstract concepts tangible. Educational apps and games introduce gamification, motivating students to practice consistently. Additionally, online worksheets and quizzes provide immediate feedback, helping students identify and correct mistakes. Technology also enables teachers to create customized lessons and track progress effectively. By integrating digital tools, educators can cater to diverse learning styles and foster a deeper connection to the material, ensuring students are well-prepared for more complex algebraic challenges.
Real-World Applications of 2-Step Equations
Two-step equations are essential in everyday tasks, such as budgeting, cooking, and construction. They help solve problems involving combined operations, making them vital for practical decision-making and planning.
6.1 Everyday Problem Solving
Two-step equations are invaluable in daily life, helping solve practical problems efficiently. For instance, calculating the cost of items on sale or determining the correct amount of ingredients for a recipe. These equations simplify tasks like splitting bills, budgeting expenses, and adjusting quantities in cooking or DIY projects. By mastering these equations, individuals can make quick, accurate decisions in real-world scenarios. Worksheets provide structured practice, enabling learners to apply mathematical concepts to everyday challenges confidently. This skill enhances problem-solving abilities, making routine tasks easier and less time-consuming. The practical application of two-step equations ensures that math remains a useful tool in navigating life’s everyday demands.
6.2 STEM Field Applications

Two-step equations are essential in STEM fields, where precise calculations are critical. In physics, they help determine velocity and acceleration. In chemistry, they aid in calculating concentrations and reaction rates. Engineers use these equations to design structures and systems, ensuring safety and efficiency. Computer scientists apply them in algorithms for data analysis and artificial intelligence. Worksheets tailored to STEM scenarios provide realistic practice, reinforcing problem-solving skills. Mastery of two-step equations enables professionals to tackle complex challenges confidently. These foundational math skills are vital for innovation and advancements in technology and science. By practicing with relevant worksheets, learners develop the accuracy and speed needed for real-world STEM applications.
6.3 Financial Literacy
Two-step equations play a crucial role in financial literacy, helping individuals manage budgets, calculate savings, and understand investments. For instance, determining total costs with tax or discounts involves multiple operations. Worksheets provide practical exercises, such as calculating loan payments or comparing pricing plans. These skills are essential for making informed decisions about spending, saving, and investing. By mastering two-step equations, individuals can better navigate financial planning, ensuring they allocate resources effectively. Worksheets tailored to real-world financial scenarios make learning engaging and relevant, preparing learners for everyday money management and long-term financial goals. This foundational math skill is vital for achieving economic stability and independence.
Assessing Understanding of 2-Step Equations
Assessing understanding involves regular quizzes, worksheet exercises, and class discussions to ensure mastery, identify learning gaps, and provide constructive feedback for improvement.
7.1 Formative Assessments
Formative assessments are essential for monitoring student progress in solving 2-step equations. These evaluations occur during the learning process and provide insights into students’ understanding. Teachers can use quizzes, class discussions, and worksheet exercises to identify strengths and areas needing improvement. Immediate feedback helps students address mistakes and build confidence. For instance, worksheets with specific problems allow teachers to track individual progress and adjust instruction accordingly. Regular formative assessments ensure that students grasp each concept before moving to more complex topics. This approach fosters a supportive learning environment and helps students develop problem-solving skills effectively. By incorporating these assessments, educators can tailor their teaching strategies to meet the needs of all learners.
7.2 Using Rubrics
Using rubrics is an effective way to assess student understanding of 2-step equations. Rubrics provide clear criteria and expectations, ensuring consistency in grading. They outline specific standards for accuracy, problem-solving strategies, and presentation. Teachers can design rubrics to evaluate worksheets, quizzes, or projects, offering detailed feedback. Rubrics also help students understand what is expected of them, fostering self-assessment and improvement. By breaking down the problem-solving process into measurable components, rubrics enable educators to identify areas where students may need additional support. This tool promotes transparency, fairness, and targeted instruction, making it invaluable for evaluating progress in solving 2-step equations. Regular use of rubrics enhances both teaching and learning outcomes.
7.3 Peer Review
Peer review is a collaborative learning strategy where students evaluate and provide feedback on each other’s work. In the context of solving 2-step equations, peer review encourages critical thinking and problem-solving skills. Students can exchange worksheets, check solutions, and discuss methods. This process fosters a deeper understanding of the equations and promotes teamwork. Teachers can guide students on how to give constructive feedback, focusing on accuracy, clarity, and problem-solving strategies. Peer review also helps identify common mistakes and strengthens communication skills. By involving students in the assessment process, it reduces the teacher’s workload and creates a supportive learning environment. Regular peer reviews can enhance retention and confidence in solving 2-step equations, preparing students for more complex math challenges.
Common Mistakes and How to Avoid Them
Common mistakes include reversing operations incorrectly and misapplying signs. To avoid these, carefully follow the order of operations and double-check each step for accuracy and consistency.
8.1 Reversing Operations Incorrectly
One of the most common mistakes when solving 2-step equations is reversing the order of operations incorrectly. For example, in an equation like (3x + 2 = 11), students often subtract 3 first instead of dividing, leading to incorrect solutions. This error stems from misunderstanding the proper sequence of inverse operations.
To avoid this, always identify and reverse the operations in the correct order. Start by isolating the variable using the inverse of the last operation performed. In the example above, subtract 2 before dividing by 3. Practicing with worksheets can help build this habit and reduce errors over time.
8.2 Miscalculations
Miscalculations are a frequent issue when solving 2-step equations, often due to arithmetic errors. For instance, students might add instead of subtract or misapply multiplication and division. These mistakes can lead to incorrect solutions, even if the steps are logically sound.
To minimize miscalculations, it’s essential to work methodically. Break down each operation, double-checking your work as you go. Using worksheets with answer keys can help identify patterns of errors, allowing for targeted practice. Additionally, teaching strategies like finger counting or using visual aids can enhance accuracy. Regular review of basic arithmetic skills also reduces the likelihood of miscalculations, ensuring a stronger foundation for solving equations effectively.
8.3 Misapplying Signs
Misapplying signs is a common error in solving 2-step equations, often occurring when students mishandle positive and negative values during operations. For example, forgetting to change the sign of both terms when moving a negative number can lead to incorrect solutions.
To address this, worksheets should include problems that highlight sign changes, such as equations involving subtraction or negative coefficients. Providing answer keys allows students to identify and correct these mistakes. Teaching strategies like color-coding or using visual aids can also help students track signs more effectively. Regular practice with targeted exercises ensures better understanding and reduces errors related to misapplying signs in equations.

Conclusion
Mastering 2-step equations is a crucial milestone in algebra, building foundational skills for more complex math. Worksheets are invaluable tools, offering structured practice and helping students identify common errors. By using answer keys and visual aids, learners can track progress and gain confidence. Consistent practice ensures long-term mastery, making these equations second nature. Encouraging students to explore online resources and customizable worksheets further enhances their learning experience. Understanding 2-step equations is not just about academics; it equips individuals with problem-solving skills vital for real-world applications. Embrace these strategies to foster a deep understanding and appreciation of algebraic concepts.



